Last Updated: 2019-07-20

Author: Jeremy Jacobson

The purpose of this codelab is to familiarize you with common concepts and terms one encounters while programming by placing them in an historical context. Along the way, we will describe at a high level how modern computers work. At the end, you will look at the computer in front of you in a new light!

What you'll learn

• Binary and Hexadecimal numbers
• Characters, ASCII, Unicode
• High vrs low level programming languages
• Compiled vrs interpreted languages

The road leading to today's computers goes back millenia. Historically, a computer was a person who makes calculations, especially with a calculating machine.

What is a computer?

For this, one should take a field trip to the Arithmeum.

Earliest examples of physical memory (The third floor of the Arithmeum)

What is the simplest way to physically represent numbers such that we may physically manipulate them in order to do arithmetic?

Counting fingers!

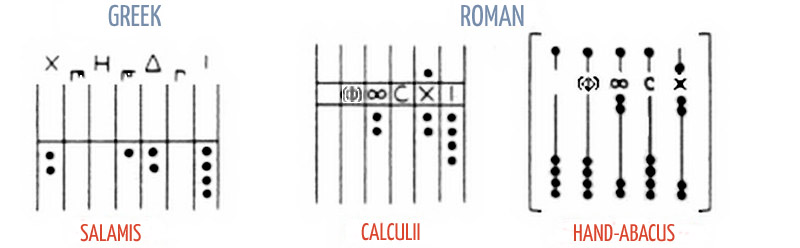
Others, dating back thousands of years, are:

• Marked stones called calculi, or marked bones
• Incan Rope counting, called Quipu
• The Abacus (See Feynmann versus the Abacus, as told by R. Feynmann)
• The same story, as told by the Abacus

The second floor of the Arithmeum (early mechanical calculators)

What do you mean mechanical?

Binary arithmetic using rockers

Slide rules and Nomograms

• A nomogram may be thought of as a generalized slide rule. The Greek word for law is nomos
• It was set up to solve just one equation that would've taken a lot of time on a slide rule, or required scales that no slide rule had
• For instance, to get the power output of a steam engine requires a nomogram with eleven different lines on it!

What do nomograms have to do with computing today?

Neural networks power deep learning and are changing a paradigm for computing that has been dominant for decades. The name is a misnomer as they are not networks but in fact parameterized families of mathematical functions. Specifically, they are piecewise linear functions. There are many interesting parallels between generalized slide rules and neural networks:

• They both represent multivariable functions on a plane
• They both offer an arbitrarily good approximation to a wide class of functions when defined on a bounded domain
• They both find ‘simple' solutions to complex problems: evaluating a neural network amounts to repeatedly taking sums, scalar multiples, and max(0,x); evaluating a nomogram requires that one draw a line.
• They both obtain this simplicity by solving problems in two phases: a difficult ‘model discovery' phase (e.g. training the neural net or finding the required nomogram), and a simpler evaluation phase.

So in these respects, computing has returned to a theme that, before electronic computers and their speed made it unnecessary, was very important for calculations. As Moore's law is now essentially over, one is led to wonder: perhaps these parallels reflect the fact that electronic computers now face the same difficulties humans have always encountered?

The first floor of the Arithmeum (four-species mechanical calculators and more)

From the Arithmeum's webpage:

The first four-species calculating machine, which means that it is able to perform all four basic operations of arithmetic, was built by Gottfried Wilhelm Leibniz. This machine can be viewed on the first floor,

• Leibniz completed his calculator in 1694
• Mechanical calculators continued to evolve
• If you took a statistics course at a university, even as late as the 1970's, you may have found yourself using the sort of mechanical calculator pictured below

Silicon Microchip Computers

Excerpts from the Arithmeum's website (link appeared earlier):

"The 1970s...were the years that saw mechanics being increasingly replaced by electronics...

...A 300-year period of development of ever more complex mechanical machines was coming to an abrupt end"

What changed?

• A transistor is a device that regulates current or voltage flow and acts as a switch or gate for electronic signals
• Just like the wooden rockers we saw earlier, but switching at the speed of light!
• Transistors are the basic elements in integrated circuits (IC), which consist of very large numbers of transistors interconnected with circuitry and baked into a single silicon microchip.
• Von Neumann architecture changed the computing paradigm.

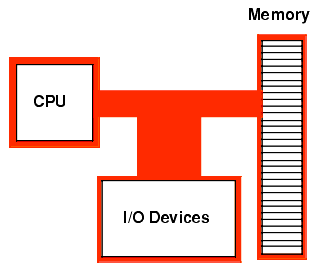
Von Neumann architecture

What follows are excerpts from a non-technical article that summarizes John Von Neumann's fascinating life and achievements. His wife, Klara Dan, was one of the world's first computer programmers.

Key points:

• The principal feature of a Von Neumann computer is that the program and any data are both stored together, usually in a slow-to-access storage medium such as a hard disk, and transferred as required to a faster, and more volatile storage medium (RAM) for execution or processing by a central processing unit (CPU).
• Since this how practically all present day computers work, the term "von Neumann architecture" is rarely used now, but it was in common parlance in the computing profession through to the early 1970s.
• When von Neumann proposed this architecture in 1945, it was a radical idea. Prior to then, programs were viewed as essentially part of the machine, and hence different from the data the machine operated on.

Digital computers understand the language of 0's and 1's called binary.

Watch the following three minute video at https://youtu.be/GcDshWmhF4A before reading more. In the video you will learn how a simple mechanical system of wooden rockers can be used to do binary arithmetic. Then note:

• Instead of rockers, in a modern digital computer we have transistors acting as switches, 1 for high voltage level and 0 for low voltage level
• Computers use binary because they can be represented by a transistor that is relatively easy to fabricate in silicon and millions of them can be put on a chip
• Each time we add another rocker, we double how many numbers can be represented, and this growth is exponential.

What is binary?

• A binary number is a number written using only digits 0 and 1
• A bit is a single binary digit. For instance, 101 has three bits and 10 two bits
• A group of eight bits is called an 8-bit byte, and sometimes is called simply a byte
• 0 represents zero, 1 represents one.
• 10 represents two
• 100 represents 4
• 1000 represents 8...

Machine code or binary code is the term used to describe any binary instruction which the computer's CPU will read and execute, e.g. 10001000 01010111 11000101 11110001 10100001 00010110. Each instruction performs a very specific task, such as adding two binary numbers together.

In the very early days of computing, programming instructions were provided in this language, which is difficult for human beings to read and write.

Chess Board Legend (Problem 1)

There is an old Indian legend about a King who was challenged to a game of chess by a visiting Sage. The King asked "what is the prize if you win?"

The Sage said he would simply like some grains of rice: one on the first square, 2 on the second, 4 on the third and so on, doubling on each square. The King was surprised by this humble request.

The Sage won.

Answer the questions below using a bash terminal.

A billion grains of rice is about 25 tonnes (1,000 grains is about 25g). Converting from grains of rice into tonnes, to fill all 64 squares in a chess board the king would need about 460 billion tonnes of rice!

In the legend, the Sage tells the King that he doesn't have to pay the debt at once, but can pay him over time by serving rice to pilgrims every day until the debt is paid off.

If you are having trouble answering the questions above, a more detailed explanation which shows how to make the necessary calculations in bash may be found in this article.

Summary

In the table below you will find the exact count of the number of grains of rice as the squares increase.

Table with grain of rice count on chessboard

So what, what is so great about 64 switches being able to represent all the numbers from 0 up to 18446744073709551615?

We can use them for more than representing numbers...they can represent characters like A or !

A character is the smallest possible component of a text, for instance A or B or / and a character is represented on a screen or on paper by a set of graphical elements that's called a glyph.

The glyph for an uppercase A, for example, is two diagonal strokes and a horizontal stroke, though the exact details will depend on the font being used. Most Python code doesn't need to worry about glyphs; figuring out the correct glyph to display is generally the job of a GUI toolkit or a terminal's font renderer.

ASCII

From https://docs.python.org/3.0/howto/unicode.html

In 1968, the American Standard Code for Information Interchange, better known by its acronym ASCII, was standardized.

• ASCII defined numeric codes for various characters, with the numeric values running from 0 to 127.
• For example, the lowercase letter ‘a' is assigned 97 as its code value.
• The ASCII value of the uppercase letter 'A' is 65.
• The ASCII value 0 is the symbol 'NUL' also known as the null byte.
• Codes 0 through 31 and 127 (decimal) are unprintable control characters. Code 32 (decimal) is a nonprinting spacing character.
• Codes 33 through 126 (decimal) are printable graphic characters.

ASCII was an American-developed standard, so it only defined unaccented characters. There was an ‘e', but no ‘é' or ‘Í'. This meant that languages which required accented characters couldn't be faithfully represented in ASCII. (Actually the missing accents matter for English, too, which contains words such as ‘naïve' and ‘café', and some publications have house styles which require spellings such as ‘coöperate'.)

Try it yourself

Write the characters of your name in ASCII.

In ASCII, everything could be stored in 7 bits. As we want to represent characters from any possible language, we will need more bits. To represent as many glyphs as possible in an efficient way, hex is used in unicode..

What is Hexadecimal?

Hex, or hexadecimal, is a number system of base 16. Hex digits are 0,1,2,3,4,5,6,7,8, 9, A, B, C, D, E, F. This number system is more commonly encountered in programming than binary.

Each hexadecimal digit maps directly into 4 bits:

0000=0,

0001=1,

0010=2,

0011=3,

0100=4,

0101=5,

0110=6,

0111=7,

1000=8,

1001=9,

1010=A,

1011=B,

1100=C,

1101=D,

1110=E,

1111=F.

Notice, given the mapping above, one hex digit is equivalent to 4 bits.

Now, lets say you have the binary sequence 1001111000001010 - it can easily be converted to hex by grouping in blocks - each block consisting of four bits.

1001 1110 0000 1010 => 9 14 0 10 which in hex becomes: 9E0A.

In particular, Hex is a neat shorthand notation for binary. Confusingly, often files consisting of hex are called binary by developers, although strictly speaking the representation is hexadecimal not binary. This is harmless since the conversion from one to the other is unambiguous.

Example

In html programming, colors are often represented by a 6-digit hexadecimal number: FFFFFF represents white, 000000 represents black, and so on.

Exercise

Conversion Table

If you've ever written some Python code and received a message such as UnicodeDecodeError: 'ascii' codec can't decode byte 0xff in position 6: ordinal not in range(128) then you have run into a problem with character sets, encodings, Unicode and the like.

• The Unicode standard describes how characters are represented by code points.
• A code point is an integer value, usually denoted in hex
• A Unicode string is a sequence of code points.
• The rules for translating a Unicode code point into a sequence of bytes are called an encoding.
• The rules for converting a Unicode character into ASCII are simple; for each code point:
• If the code point is < 128, each byte is the same as the value of the code point.
• If the code point is 128 or greater, the Unicode string can't be represented in ASCII encoding. (Python raises a UnicodeEncodeError exception in this case.)

The full list of code points can be found at http://www.unicode.org/charts/

What is UTF-8?

Unicode Transformation Format 8-bit (UTF-8) is a variable-width encoding that can represent every character in the Unicode character set.

Python supports writing source code in UTF-8 by default:

• \xnn - specifies a two digit hex unicode 'code point'.
• \unnnn - specifies a four digit hex unicode 'code point'.
• \Unnnnnnnn - specifies an eight-byte hex unicode 'code point'.
• The full number of digits must be used, padded with leading 0's.

Try it yourself

Write your name in Unicode (UTF-8). What is your favorite code point?

Now that we understand binary, we can finish our high level overview of how we program by describing how instructions are passed to a computer.

The genesis of programming

Early digital computers

The earliest digital computers where Konrad Zuse's Computers. In the year 1943 he gave the following definition: Computing is the deviation of result specifications to any specifications by a prescription. What does this mean? In a word, they were programmable!

In particular, they were designed to read arbitrary binary instructions from a punch tape (they should work in the binary digit system because Zuse wanted to contruct his computer with binary switching elements), and not only the numbers should be represented in a binary form, but the whole logic of the machine should work in a binary switching mechanism (0-1-principle)!

From this definition, Konrad Zuse defined the architecture of his computers Z1, Z2, Z3 and Z4. The Z4 is pictured below. It had 512 bytes of memory.

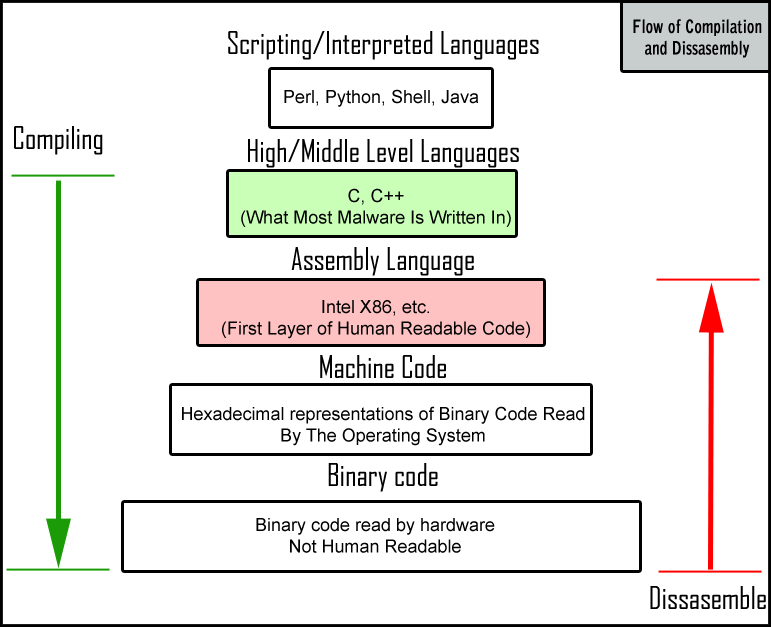
What is assembly language?

An assembly language is a programming language that enables a programmer to use human-readable text to write machine code.

From a stackoverflow comment:

My grand father was working with a Z1. The modus operandi was to write down your code in assembly language on paper and the secretary would actually do the transcription (to binary) to punch cards, then pass them to the machine operator and the result would be handed back the morning after.

In particular, the first assemblers were human!

Here are some assemblers at work.

When programming modern computers, these details, which are specific to the hardware are hidden from the programmer in low level languages such as Intel X86.

High level languages are designed to allow humans to efficiently write powerful programs. Ideally, they do not require the programmer to think about hardware details, that is, the same code should work on many different types of hardware (Intel vrs AMD, 64-bit vrs 32-bit, etc.) and operating systems (Linux, Windows, Mac).

High and low level languages

Compiled vrs interpreted languages

Besides high vrs low level languages, there is a further distinction.

Roughly speaking, compilation is the process of converting human readable code such as C++ into binary instructions. Compiled languages require this step when programming: first code, then compile, then run the compiled code as many times as you want.

Interpreted languages run inside of a program that interprets the commands and executes them immediately. Since the conversion to binary step is happening everytime you run the code, these languages are generally slower, although there are tricks (e.g. using these Python to wrap C++ or Fortran code) that make this a non-issue in some applications.

Other examples of popular compiled languages

• Fortran
• Go

Congratulations, you've competed essential computer literacy!

You now know the key concepts that make modern computers work and allow us to program them.

Further reading

• https://docs.python.org/3/library/dis.html

Reference docs

• https://www.arithmeum.uni-bonn.de/
• https://cython.org/